本文为作者原创,欢迎分享,若需转载请联系微信(ddupxyz),谢谢!
灵感也不过是熟中生巧,长期锻炼的结果。
---- 朱光潜《谈美书简》
一、缘由
孩子刚上小学,与学习直接相关的事也越来越多了,除了日常的生活习惯外,也希望引导她去养成更好的学习习惯,早点掌握学习的元技能:如何学习!
从哪一块入手呢?
日常和女儿玩耍时,经常会和她玩你问我答的小游戏,话题基本上与她最近学习或阅读的内容相关,她会来考我,我也会去考她,效果还挺不错的~ 但在这个过程中发现一个问题,刚学的内容一般都记得很清楚,除了极个别外,大部分内容过段时间就模糊了,要么记混,要么就忘了。
如何通过更科学的方法来学习和记忆,让学习的内容从短时记忆转到长时记忆?恰好这一块有一点点经验,不过之前没有去系统梳理过,也没想过可以帮助孩子更好地去学习。
经过一段时间的实践,发现效果挺好的,分享出来 ~ 带娃的家长可以试试(当然,成人同样可以用,我也用这个方法在背宋词,学英语,甚至学数学)
该方法基于三部分内容:
- 艾宾浩斯遗忘曲线(Ebbinghaus' Forgetting Curve)
- 间隔重复理论(Spaced Repetition)
- 莱特纳学习方法(Leitner Learning Method)
每部分都值得详细说说。
二、艾宾浩斯遗忘曲线
在一段较长的时间内多次学习(间隔重复),而不是在短时间内反复学习,学生更容易记住或学会这些内容。
---- 赫尔曼.艾宾浩斯
很多人都知道艾宾浩斯遗忘曲线(Forgetting Curve),就是长得像下面这样的一条线,这一曲线最早由德国著名的心理学家赫尔曼.艾宾浩斯(Hermann Ebbinghaus)通过 1880 年到 1885 年之间的一些实验提出。
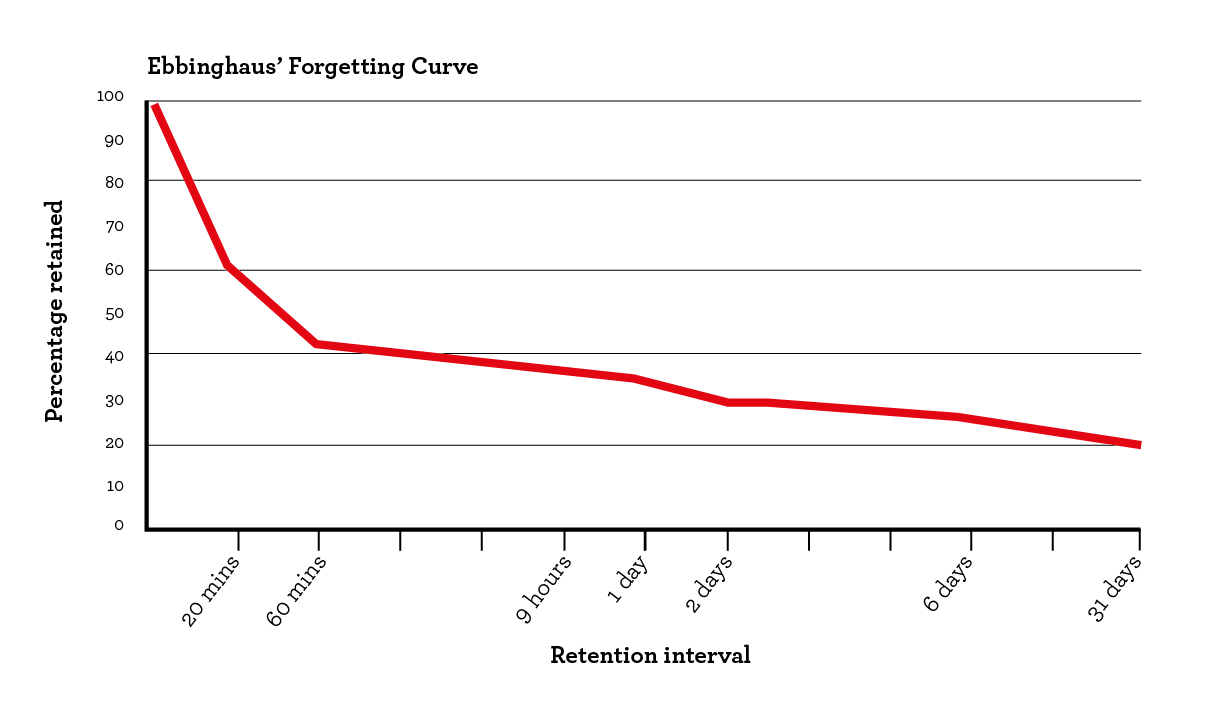
艾宾浩斯遗忘曲线提示了这样的遗忘规律,遗忘是先快后慢的,在学习后最初的 24 小时,你会忘掉绝大部分学到的内容,但一天之后遗忘速率就变得平缓了,大致有下面这样的结论:
- 20 分钟后,42% 被遗忘掉,58% 被记住。
- 1 小时后,56% 被遗忘掉,44% 被记住。
- 1 天后,74% 被遗忘掉,26% 被记住。
- 1 周后,77% 被遗忘掉,23% 被记住。
- 1 个月后,79% 被遗忘掉,21% 被记住。
当然,遗忘的速率除了与时间相关外,学习的内容是否感兴趣,是否有重要意义,是否情感相关都有很大关系,我们在这里只讨论时间这个重要的因子,内容相关影响另开主题讨论。
自然会想到,如果在上面的几个关键时间点(20 分钟、1 小时、1 周、1 个月)加入复习,记忆的巩固效果肯定会更好(本质上是完成从短时记忆到长时记忆的转换)。
事实也确实如此,而且有不少认知心理学家在这方面积累了很多实验成果。其中最著名的一个成果就是间隔重复(Spaced Repetition)效应。
三、间隔重复理论(Spaced Repetition)
Repetition is the key to real learning.
重复是真正学习的关键所在。
---- Jack Canfield
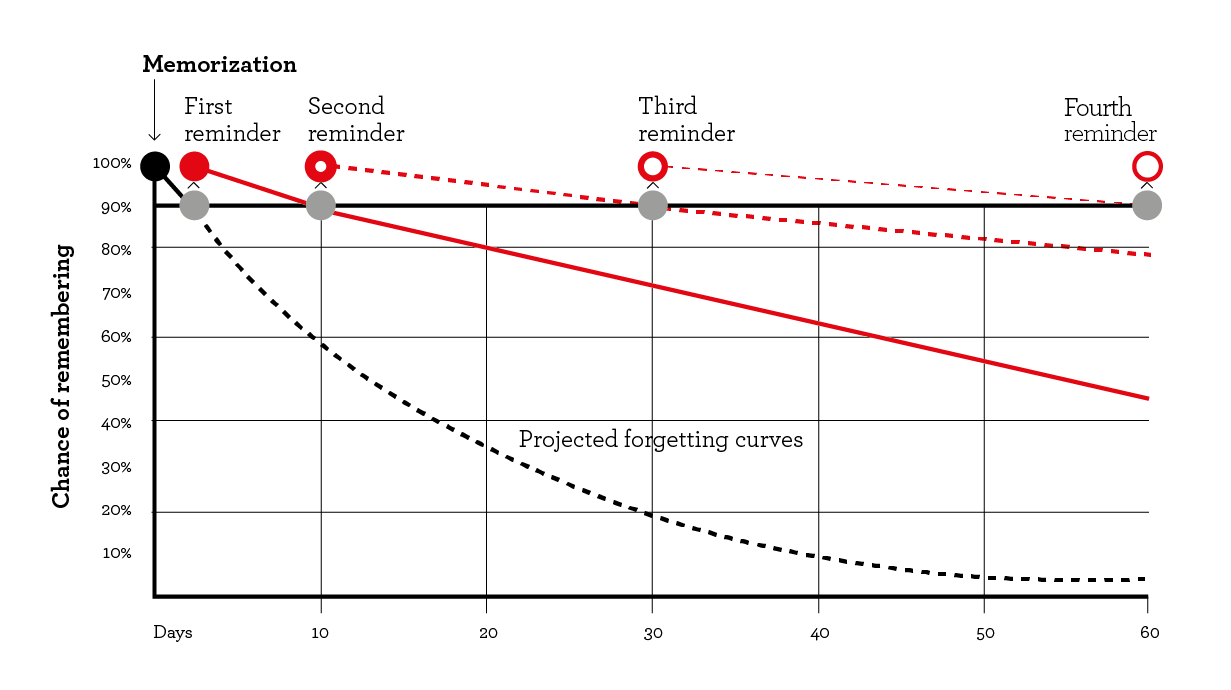
为了减缓遗忘的速度,每隔一段时间,重新回顾之前学习的内容,可以极大帮助我们记住更多的内容。经过间隔重复的巩固学习后,遗忘曲线就变成了上面的样子,可以看到,通过间隔重复学习,我们可以将记忆留存的准确率提升到 90% - 100%,这样的结果还是很令人振奋的。
简单来说,间隔重复(Spaced Repetition)是一种利用心理学间隔效应,通过不断复习所学内容并逐步增加两次复习间的时间间隔来提升效率的学习技巧。
我们可以利用间隔重复效应来学习几乎任何东西,从背单词到记诗词,从记术语到熟练掌握数学公式,大量示例都证实了非常有效。
关于间隔重复,有个很关键的问题:间隔重复的频率如何确定?
要回答这个问题,不得不提到一个人,彼得.沃兹尼亚克(Piotr Wozniak),1982 年,彼得还是个大学生,他遇到了很多学生都会遇到的一个问题,要学习大量的学习材料,而令人沮丧的是,每次考完试,所有学习的内容很快就忘记得差不多了。
彼得花了大量的时间研究如何减少遗忘这个问题,并尝试以问答的方式,在不同的时间间隔去学习,在大量的实践过程中,彼得不断优化和迭代他的间隔重复算法,这些算法影响了现今许多与抽认卡(Flashcard)学习相关的工具软件。
基于自己的研究,彼得还与朋友一起成立了 SuperMemo World 公司,并发布了 SuperMemo 应用程序,一直以来 SuperMemo 在间隔重复算法方面都是非常领先的。我们经常听到的卡片记忆工具 Anki 也是基于 SuperMemo 当初的 SM-2 算法(SuperMemo 的算法现在已经更新到 SM-17 了)。下面这张图是彼得当时通过间隔重复去学习的一张记录图。

不过,这里我们暂时不关心背后复杂的算法实现,我们只是需要找到一种简单有效、更易执行的方式去实践间隔重复学习就可以了。
接下来要分享的莱特纳盒子(Leitner Box)就是一种很好用的间隔重复练习方法,下面来介绍一下。
四、莱特纳学习法
我们塑造了工具,而后工具也在塑造我们。
---- 麦克卢汉
塞巴斯蒂安.莱特纳 (Sebastian Leitner) 和艾宾浩斯一样,也是一名德国的心理学家(1919-1989)。莱特纳在 1970 年左右出版了他的重要著作《So lernt man lernen (How to learn to learn)》,在这本书中,他引用了艾宾浩斯的遗忘曲线,发明了以他自己名字命名的盒子:「莱特纳盒子(Leitner Box)」,也就是他书中说到的学习卡片箱,这是一种利用「间隔重复」的来提升学习效率的间隔练习体系。
1. 抽认卡(Flashcard)
抽认卡也称闪卡(Flashcard),是由莱特纳在 20 世纪 70 年代提出的,他建议把学习的内容进行拆分,分成一张一张独立的问答卡,正面是问题,背面是答案,学习者可以通过能否回答出卡片的问题来判断这张卡片的内容是记住了还是没有记住。
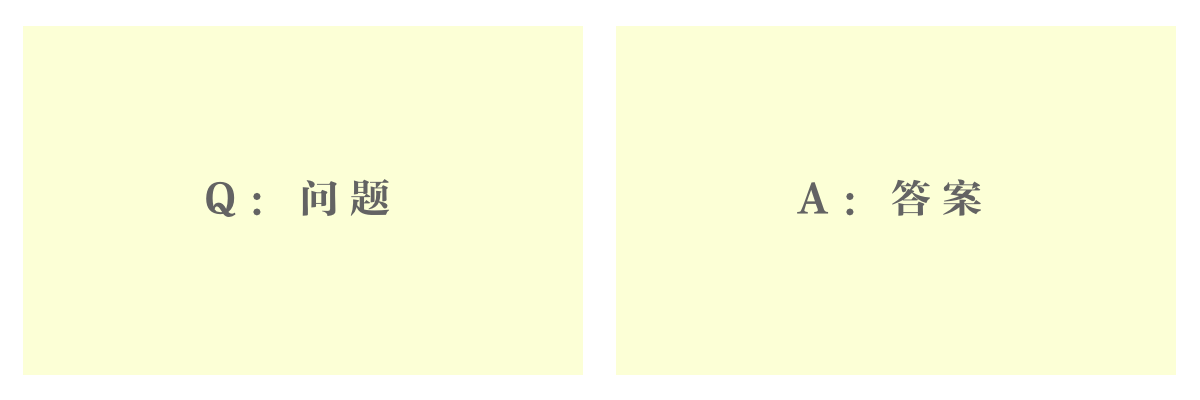
现在也有很多支持电子闪卡的软件工具,最著名的应该是 Anki。本文主要讨论实体卡片,更适合孩子使用。
2. 莱特纳盒子(Leitner box)
为了管理这些卡片,莱特纳建议可以制作像下面这样的一个学习卡片箱,也称为莱特纳盒子 (Leitner Box)。
卡片箱一共 5 格,格子里面放要学习的抽认卡,其中 1 号格子中的卡片内容最为生疏,巩固复习的频率更高;2 号格子其次,越后面格子里的卡片越熟练。
我们在使用时,以复习 3 号格子里的卡片内容为例,从 3 号格子里抽出一张卡片,通过问答进行测试,如果这张卡片的内容已经掌握,就把它放到 4 号格子里(升级);如果这张卡片的内容没有掌握,则把这张卡片放回 2 号格子(降级到前一个格子)。
另一种方法是将记不住的卡片直接放回到 1 号格子(降级到 1 号格子)。
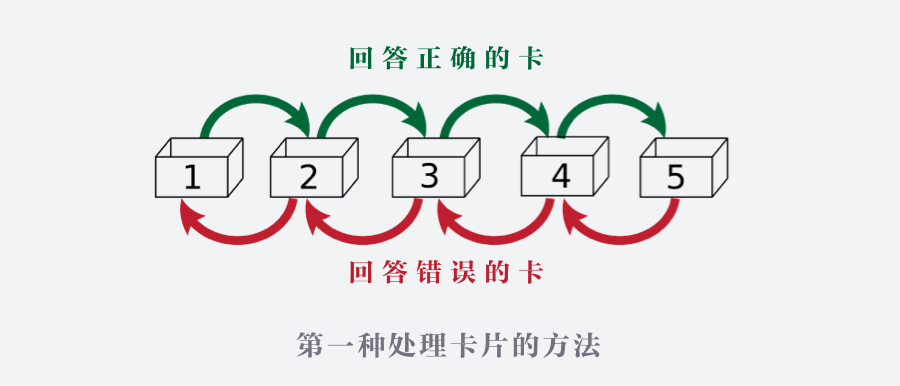
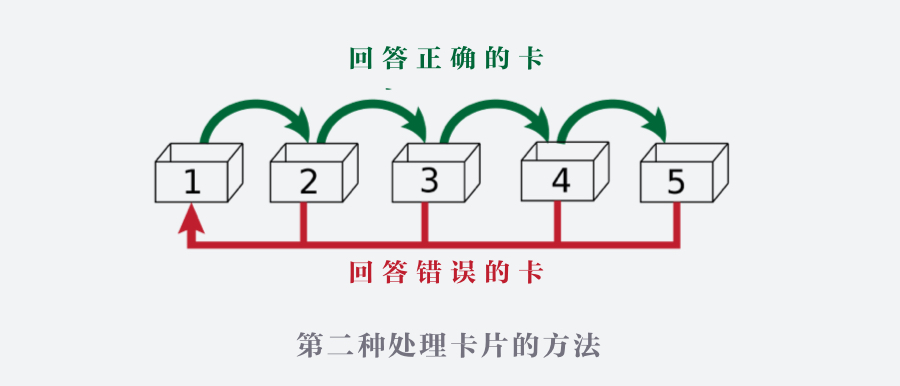
规则是:只有当一个格子放满了卡片,才会复习这个格子里的卡片。莱特纳盒子中的每个格子厚度都不一样,这就决定了越在前面格子里的卡片复习的频率就越高。
莱特纳盒子在利用间隔重复效应提升学习效率方面改进了很大一步,但仍然存在一些问题,比如说,卡片复习的频率应该与时间相关性更高,通过装满格子来决定卡片复习的频率这种间接的方式并不太准确(在下面的实践介绍里我们可以通过间隔重复算法表来完美解决这个问题)。
下面来分享一下我带女儿通过莱特纳盒子进行学习的一些经验,这些实践一方面参考了别人的一些经验分享,另一方面是自己在实践中不断迭代后的总结。
五、莱特纳学习法实践
1. 卡片的选择
卡片,我选择的是最普通的一种索引卡,搜索「index cards」就可以找到,一般有多色、横线或网格的不同类型,我选择的是下面这种多色的横线版,76mm X 126mm 高宽,大小也比较合适。

2. 卡片的书写
卡片的内容不限,可以是诗词、英语、文化常识,甚至一个数学知识点。目前给女儿的卡片这几类都涉及到了。
在写卡片前,有几点需要注意
- 内容原子化。一张卡片只写一个点,问和答表述清楚。这是一个粒度划分的问题,很多人刚开始写卡片的时候,会像平时记笔记一样,将很多个要点都写在一张卡片,这样其实不利于记忆以及后面的复习。
- 记录日期。记下写这张卡片时的日期,写日期主要是为了在任何时候一旦抽出一张卡片,就能知道这个知识点是在什么时候产生,对学习的推进有一个时间维度上的观测和把控。
- 注明来源。写上这张卡片内容的来源。这点非常重要,主要是为了帮助你在回顾的时候查考来源,更加方便去验证,了解上下文更多。
下面是女儿正在使用的卡片示例,因为她才一年级,所以目前的卡片都是由我来帮忙书写的,稍大一点,由她自己来书写会更好。



3. 莱特纳盒子的制作
本来准备自己动手用鞋盒来制作的,结果去某宝逛了一圈,意外的找到了非常适合直接拿来使用的盒子,而且 7 格的设计也刚好匹配上后面的间隔重复算法,完美。可能店家也想不到会有人拿来这样用吧,大部分人买回去都是拿去装像钥匙、证件,甚至袜子这样的小东西。
拿回家装好,贴上标签,一个完美的莱特纳盒子就完成了,取了个名字「书姐的学习盒子」,感觉上还挺好的。

4. 间隔重复算法表
使用莱特纳盒子来学习,很关键的一环是,我怎么快速知道今天应该复习哪个格子里的卡片?有支持相关算法的软件工具可以帮助计算,而经过几轮实践,最终自己制作了下面这样的间隔重复算法时间表,打印出来,非常好用!
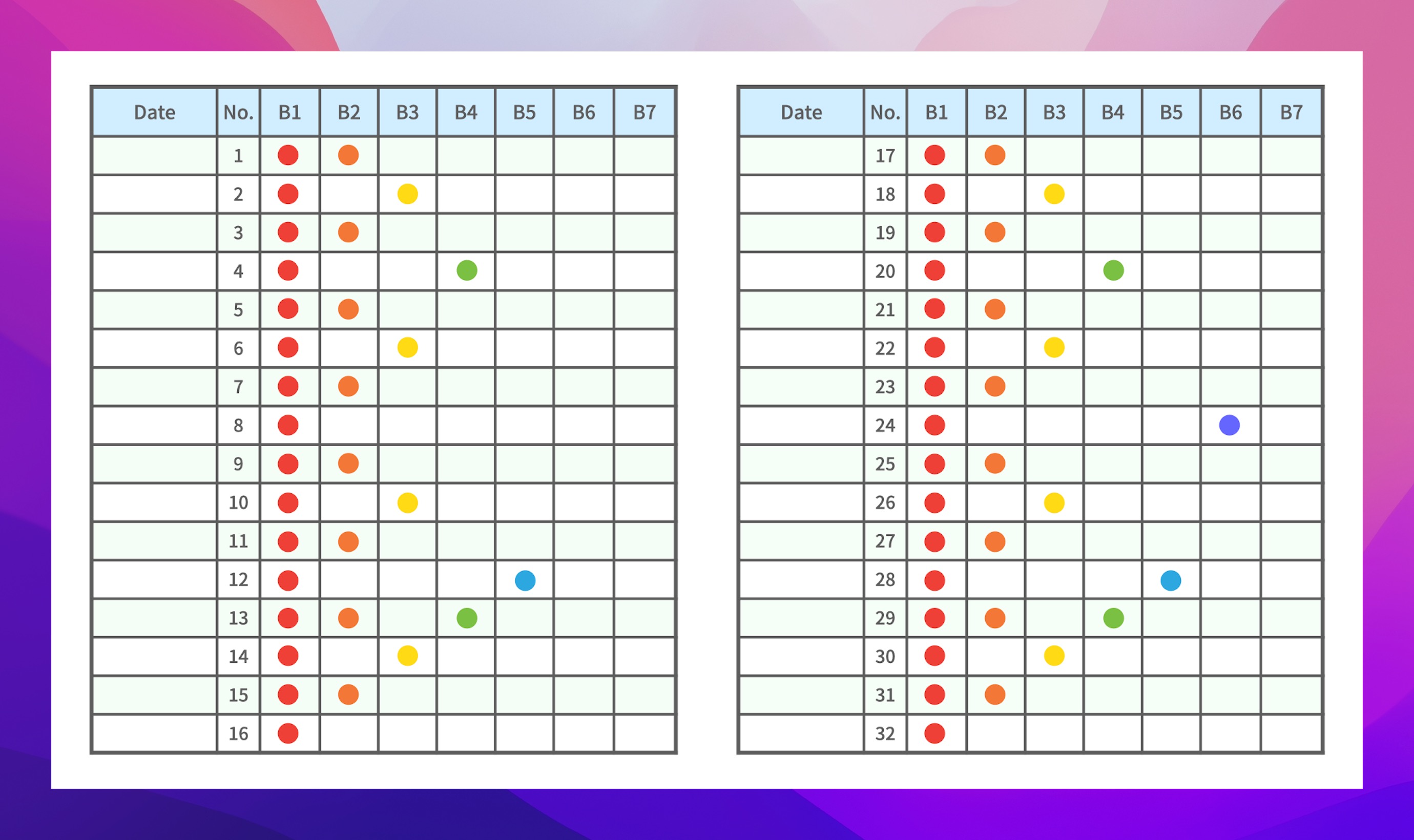
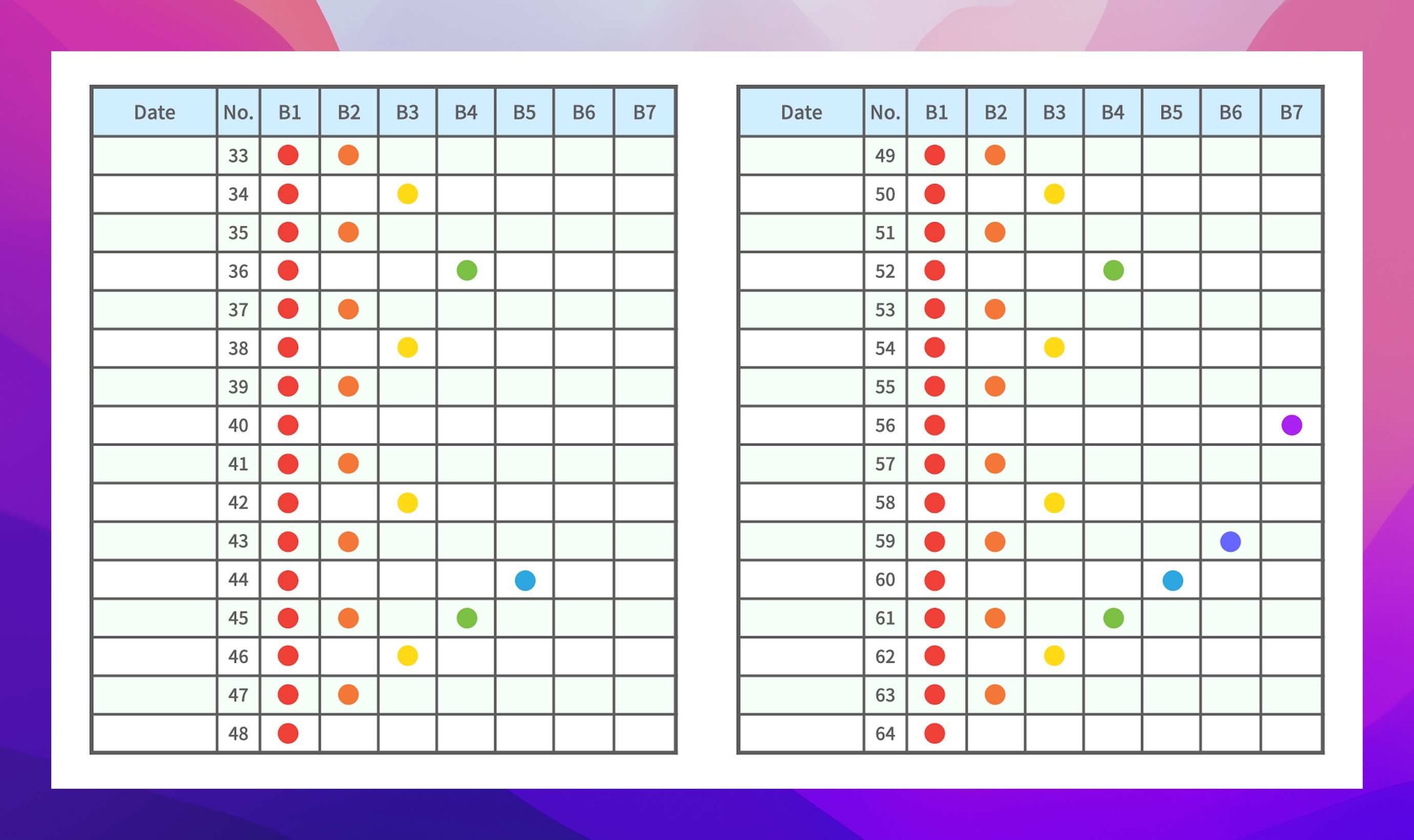
这两张图示看着有点复杂,给大家解释一下,其实很简单:把一个大的复习周期设定为 64 天,每天应该复习哪个格子里的卡片已经事先预定好了,直接查找后去执行就可以了。
举个例,假如说今天是这个复习周期的第 20 天,对应上面的表格,可以快速的查到,第 20 天应该复习 B1(格子 1) 和 B4(格子 4) 里的卡片,简单快速。
六、每天的使用流程
一般来说,我会每天抽一个比较固定的时间来和女儿一起过一遍 「书姐的学习盒子」中的内容。
1. 新卡片制作
我一般会在头一天根据当天学习的情况,制作新的抽认卡,并放到 B1,B1 里的卡片不应该特别多,不超过 5 张最好(只是一个经验值)。
2. 根据算法复习卡片
拿出 「间隔重复算法表」,找到当天日期及对应应该复习的盒子编号。
比如说今天(2022-05-06),刚好是这轮学习周期的第 20 天,快速一查,立刻知道今天应该复习 B1(1 号盒子) 和 B4(4 号盒子) 里的卡片。
先从编号靠后的盒子开始复习,那这里就应该先复习 B4 里的卡片,从中任取一张,如果能顺畅记住,就把这张卡片放到 B5;如果记不住,可以多熟悉一下,再把这张卡片放回到 B3。
然后再来看 B1 格子里的卡片,同样,能顺畅记住的就放到 B2,记不住的话多记几遍,仍然留在 B1。
随着时间的推移,整个卡片从左边的盒子往右边的盒子推移,最终会汇入 B7,当一张张卡片进入到 B7 时,恭喜你!因为 B7 里的这些卡片内容你已掌握得非常熟练(已经进入长时记忆),可以归档了。
随着被归档的卡片越来越多,那种累积的成就感是无与伦比的。
七、更多思考
目前的抽认卡片仍然比较独立,因此从学习的角度来说仍然是知识点复习为主,记忆偏多。有了这个基础,未来还可以朝向卢曼卡片学习法过渡,卡片与卡片之前建立联系,知识形成网络,网络涌现创造,真正从记忆学习系统转向学习创造系统。
八、常见问题
1. 电子卡片与实体卡片优劣?
关于实体与电子卡片,经过实践下来,对于孩子学习来说,实体卡片完胜,抽出和放入卡片的感觉是非常好的,每个格子大概多少张卡片也一目了然,而且家长还以可和孩子一起玩你问我答的卡片游戏。
电子卡片当然有自己的优势,更适合成人使用,从记忆的角度来说,使用像 Anki 这样的工具,内置了间隔重复算法,直接使用即可,每天会自动提示你应该过的卡片,很方便。
再一步,如果想使用像卢曼卡片这样的学习方法,使用电子卡检索更方便,知识点关联也更容易实现,更适合成人作为卡片学习创造系统,我自己现在就是用 Obsidian 作为自己的卡片学习创造系统,使用效果也非常好。
2. 每天卡片生成的数量与复习所花时间是多少?
以自己带女儿学习的数据来看,平均每天会产生 2 ~ 5 张卡片,每天花在学习盒子上的时间在 20 分钟左右,不会有太大压力,节奏感也不错,效果却很明显。
3. 卡片内容仅限于记忆类的内容吗?
不一定,尽管抽认卡(Flashcard)很适合记忆类的内容,但在实践中,也引入过像一些数学思维的小任务,完全没问题。
但抽认卡确实不太适合那种发散性的问答,因为发散性的问题没有一个明确的检验标准,很难判断掌握得熟练还是不熟练,整个流程的推进就不会太顺畅。
九、拓展阅读
- How To Remember Anything Forever-ish
- How the SuperMemo Method Works - A Comprehensive Guide
- 卢曼卡片盒笔记法介绍 (Introduction to the Zettelkasten Method)
- How to Remember More of What You Learn with Spaced Repetition
- Spaced Repetition for Efficient Learning
前面的间隔重复算法表是自己制作的模板,如果需要可打印的高清 PDF 以及盒子相关的购买链接,可以加我微信(ddupxyz)或发邮件 [email protected] 索取,麻烦注明你的用途,我可以发你!